Hello!
Several years ago we already shared this kind of solver, but last time our demonstration framework was not very compelling (for example, it was lacking collision detection and hence only very basic scenes with constraint force limits could be tested) - so I decided to revisit it now as I've got some free time, and quickly wrote a testbed that compares PGS with CG-based solver. PGS comes in two flavors - classic and shuffled - the last one allows to use various schemes to permute constraint rows each iteration, for example random shuffling, even-odd shuffling and so on.
Our solver is based on the MPRGP (Modified Proportioning with Reduced Gradient Projections) by Z. Dostál; we modified the original MPRGP to support box limits (low/high, instead of just lower limit), and incorporated preconditioner that is fairly cheap - double (left+right) Jacobi preconditioner. Solver also benefits from the J*M^-1*J^T decomposition that significantly speeds up matrix-vector multiplications.
Additionally, I added a hack to make joints more stiff, which is similar to shock propagation in a way - constraint masses are scaled locally for each joint, allowing to setup open loop systems where scales are set so that impulse propagates better from root to nodes. It is still a hack with artifacts, for example stack is still becoming unnaturally resistant to tumbling with large mass scaling parameters - but quite tolerable for mass scaling of, say, 2. The aim of that testbed was to see what solver matches which situation better, and using hacks seems alright for real-time game simulation.
The old speculations were somewhat confirmed - for fast real-time systems where quality/accuracy is not the goal - PGS still works better, as it guarantees lower error each iteration, and can behave reasonably well with even very low iteration count, another plus is that each iteration is very lightweight. Local mass scaling can help pretty noticeably even with relatively low mass scaling parameters.
In the systems where accuracy/joint stiffness is required, CG-based solver fits much better. And although each iteration is heavier than one iteration of PGS, and the method requires spectral radius estimation (additional overhead), ultimately it converges faster with larger iteration counts (>50), and for stiff systems provides better behavior within the same frametime. The method is also naturally parallel, contrary to PGS which requires coloring or splitting, so it will benefit from GPU acceleration (which we also experimented with several years ago and got significant speedup even on GTX260-era HW). Additional note, however, is that the solver calculates allowed stepsize each iteration, so it should definitely benefit from the island detection (rather than solving all the islands in a single system).
The project also incorporates FEM-based deformables (corotational FEM constraints that fit into the very same system with the regular rigid body joints, so coupling is natural), which comes in handy when testing stiff systems.
For anybody interested, source code is available on github - but the render uses Vulkan API, so LunarG Vulkan SDK installation is required (details in the readme.md file). Our old paper, describing both our approach to formulating FEM-based constraints (which actually very similar to the one by M. Servin et al., from "Interactive Simulation of Elastic Deformable Materials") and the CG-based MLCP solver, is also available on github.
Conjugate Gradient based MLCP solver source
-
avoroshilov
- Posts: 4
- Joined: Fri Jan 05, 2018 5:30 am
-
Dirk Gregorius
- Posts: 861
- Joined: Sun Jul 03, 2005 4:06 pm
- Location: Kirkland, WA
Re: Conjugate Gradient based MLCP solver source
Thanks for sharing!
-
Erwin Coumans

- Site Admin
- Posts: 4221
- Joined: Sun Jun 26, 2005 6:43 pm
- Location: California, USA
Re: Conjugate Gradient based MLCP solver source
Thanks for sharing this, I'll give it a spin. Hopefully it is reasonably easy to build.
I wonder how the solver compares with the NNCG solver, which is a hybrid of PGS and CG? We have some implementation but it is mainly useful when the problem requires a very high iteration count in PGS.
I wonder how the solver compares with the NNCG solver, which is a hybrid of PGS and CG? We have some implementation but it is mainly useful when the problem requires a very high iteration count in PGS.
-
avoroshilov
- Posts: 4
- Joined: Fri Jan 05, 2018 5:30 am
Re: Conjugate Gradient based MLCP solver source
Dirk Gregorius, Erwin Coumans
Glad to share!
I remember Dirk asked about the NNCG last time we shared our demos, but I didn't have time to implement NNCG back then, or even look too closely. Now, I have that on the list of things to do, and if I'll get to it, I will share the results.
From the very high level overview, I can only say that our algorithm stays within the feasible set at all times, while NNCG seems to be able to step out in some cases (when the intermediate solution is close to boundaries, but was not at previous frame, thus having nonzero gradient/residual pointing away from the feasible set) until the next PGS projection is performed.
And with (-inf;+inf) for all constraints limits (basically, linear system, not LCP) our algorithm should boil down to straightforward CG iterations, while the NNCG is a mixture of PGS+Conjugate Directions (or rather, Fletcher-Reeves nonlinear Conjugate Gradient). I believe in this case the convergence of the latter could be slightly worse, as in case of e.g. FEM or other purely linear system the underlying cost function will be quadratic.
But it case of complex MLCP it is hard to immediately see whether our expansion/proportioning will be beneficial over the PGS + F-R NCG, so I guess I'll leave it for future experiments.
Our method is also losing to PGS in the very limited iteration count scenarios, so the question would be will it behave better than NNCG in scenarios where accuracy matters more. One thing to note here - our method comes with the preconditioner (which improves convergence quite a fair bit), but I think the same logic could be applied to the NNCG as well, although maybe not as straightforward.
We also require the matrix spectral radius to be estimated, but in complex scenarios, and especially when parallelized, this doesn't introduce too much of an overhead typically, although might matter if our methods will be very close in terms of accuracy/time ratio.
Parallelization is very important, and our method is fully-parallelizeable (i.e. could be split into several highly parallel steps per iteration), while the NNCG presented incorporates PGS which has known parallelization issues such as coloring/splitting requirements, and in case of coloring - additional jittering due to colorization changing order of solving constraints.
Glad to share!
I remember Dirk asked about the NNCG last time we shared our demos, but I didn't have time to implement NNCG back then, or even look too closely. Now, I have that on the list of things to do, and if I'll get to it, I will share the results.
From the very high level overview, I can only say that our algorithm stays within the feasible set at all times, while NNCG seems to be able to step out in some cases (when the intermediate solution is close to boundaries, but was not at previous frame, thus having nonzero gradient/residual pointing away from the feasible set) until the next PGS projection is performed.
And with (-inf;+inf) for all constraints limits (basically, linear system, not LCP) our algorithm should boil down to straightforward CG iterations, while the NNCG is a mixture of PGS+Conjugate Directions (or rather, Fletcher-Reeves nonlinear Conjugate Gradient). I believe in this case the convergence of the latter could be slightly worse, as in case of e.g. FEM or other purely linear system the underlying cost function will be quadratic.
But it case of complex MLCP it is hard to immediately see whether our expansion/proportioning will be beneficial over the PGS + F-R NCG, so I guess I'll leave it for future experiments.
Our method is also losing to PGS in the very limited iteration count scenarios, so the question would be will it behave better than NNCG in scenarios where accuracy matters more. One thing to note here - our method comes with the preconditioner (which improves convergence quite a fair bit), but I think the same logic could be applied to the NNCG as well, although maybe not as straightforward.
We also require the matrix spectral radius to be estimated, but in complex scenarios, and especially when parallelized, this doesn't introduce too much of an overhead typically, although might matter if our methods will be very close in terms of accuracy/time ratio.
Parallelization is very important, and our method is fully-parallelizeable (i.e. could be split into several highly parallel steps per iteration), while the NNCG presented incorporates PGS which has known parallelization issues such as coloring/splitting requirements, and in case of coloring - additional jittering due to colorization changing order of solving constraints.
-
avoroshilov
- Posts: 4
- Joined: Fri Jan 05, 2018 5:30 am
Re: Conjugate Gradient based MLCP solver source
Btw, Erwin, you mentioned very high iteration counts - that depends on the definition of very high. At the scene of box stacking there is clear benefit of our solver over the PGS at 30 iterations, and generally it depends on the scene complexity: the more complex the scene, the more iteration our solver requires to converge to a solution that is not temporally noisy (well, not noticeable at least). And as soon this convergence point is reached, the solver is a benefit over PGS. It is that PGS when iteration count is really insufficient becomes less stiff, and this is far more plausible - perceptually a win.
-
avoroshilov
- Posts: 4
- Joined: Fri Jan 05, 2018 5:30 am
Re: Conjugate Gradient based MLCP solver source
Got some free time recently, and implemented NNCG. It is quite good, I must say.
As expected, it is a little bit worse in terms of pure linear system convergence (pasting as URL since I couldn't make the BBcode width to work here):
https://raw.githubusercontent.com/avoro ... NNCG85.png
red - PGS 180 iterations, green - our CG-based solver 90 iterations (plus, 15 power iterations to estimate spectral radius), blue - NNCG 127 iterations. Approximate timing of 20ms on Core i7-6500U in all three cases.
I also wanted to check the convergence with min/max lambda (i.e. the true MLCP case), and didn't think of anything better than the same FEM beam falling onto inclined plane, and sliding due to low friction contacts. This resulted in the following convergence graph (please note iterations 1-15 are omitted in the graph):
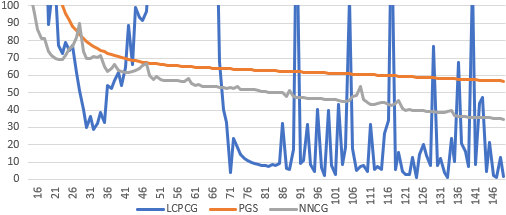
The graph shows projected gradient norm, and our solver experiences spike around iterations 40-65 - that is somewhat expected, although typically spikes are much narrower; but the spike falls under the convergence curve bound. Otherwise, NNCG shows better behavior than PGS (with comparable implementation simplicity), and our solver shows better convergence, if consider local minimum of the gradient norm (i.e. turn blind eye to spikes).
So generally, seems like PGS is a winner in cases where absolute minimum resources are allocated to solve the MLCP (<10 iterations), NNCG is good for something in-between (10-60 iterations), and our solver suits accuracy demanding cases best (60+ iterations).
There is another potential benefit in our solver which I already mentioned - it is inherently parallel, i.e. it will benefit from GPU acceleration the most of three solvers presented.
On the other hand, NNCG is much easier to implement than our solver (I mean sequential/SIMD implementations).
Hope this sheds some light on how our solver compares to NNCG
As expected, it is a little bit worse in terms of pure linear system convergence (pasting as URL since I couldn't make the BBcode width to work here):
https://raw.githubusercontent.com/avoro ... NNCG85.png
red - PGS 180 iterations, green - our CG-based solver 90 iterations (plus, 15 power iterations to estimate spectral radius), blue - NNCG 127 iterations. Approximate timing of 20ms on Core i7-6500U in all three cases.
I also wanted to check the convergence with min/max lambda (i.e. the true MLCP case), and didn't think of anything better than the same FEM beam falling onto inclined plane, and sliding due to low friction contacts. This resulted in the following convergence graph (please note iterations 1-15 are omitted in the graph):

The graph shows projected gradient norm, and our solver experiences spike around iterations 40-65 - that is somewhat expected, although typically spikes are much narrower; but the spike falls under the convergence curve bound. Otherwise, NNCG shows better behavior than PGS (with comparable implementation simplicity), and our solver shows better convergence, if consider local minimum of the gradient norm (i.e. turn blind eye to spikes).
So generally, seems like PGS is a winner in cases where absolute minimum resources are allocated to solve the MLCP (<10 iterations), NNCG is good for something in-between (10-60 iterations), and our solver suits accuracy demanding cases best (60+ iterations).
There is another potential benefit in our solver which I already mentioned - it is inherently parallel, i.e. it will benefit from GPU acceleration the most of three solvers presented.
On the other hand, NNCG is much easier to implement than our solver (I mean sequential/SIMD implementations).
Hope this sheds some light on how our solver compares to NNCG