Algorithm help / Connecting Centroids
-
AstroCoder
- Posts: 3
- Joined: Sat Aug 26, 2017 8:49 pm
Algorithm help / Connecting Centroids
Hello and Greetings! New to this forum. My background is astronomy and computer programming.
I'm working on a PBD project and I'm trying to develop an algorithm to connect certain points with other points. What I've done is taken the PBD software from GitHub, and have modified the Demo example called 'GenericConstraintsDemos'. I've taken all contraints out except the distance constraint. I've also forced the simulation to work on a 2D plane with the intention of extending to 3D eventually.
Please refer to the following diagram:
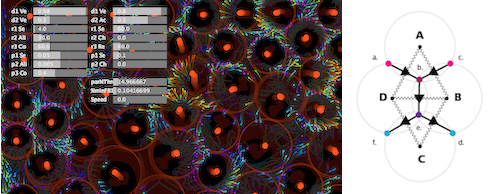
So as you can see in this example, there are nine circles. The simulation allows for any number of circles, but I'm trying to make this post as simple as possible for starters. The green dots represent the centers of the circles; the red dots represent the centroids of the three adjacent/connected circles; the black dots represent some intersections (I call these the "outer" intersections) between circles; and the blue lines connect either centroids with other centroids, or centroids to intersections in a particular pattern. In the simulation, the radii of the circles can change and, since I'm applying a distance constraint, the varying sizes of the circles causes the locations (and existence) of the dots and lines to change.
The code that I have at this point is able to identify/calculate the locations of the black dots and the red dots, but I'm having trouble coming up with an algorithm that correctly connects the red and black dots. The diagram I've attached shows the correct connections, but coming up with an algorithm to do this automatically and as the simulation runs has me stumped.
I'll also add that each circle knows which other circles it's in contact with, and what those intersection points are.
Has anyone come across this problem and maybe give me some help?
Thank you and Cheers,
AstroCoder
I'm working on a PBD project and I'm trying to develop an algorithm to connect certain points with other points. What I've done is taken the PBD software from GitHub, and have modified the Demo example called 'GenericConstraintsDemos'. I've taken all contraints out except the distance constraint. I've also forced the simulation to work on a 2D plane with the intention of extending to 3D eventually.
Please refer to the following diagram:
So as you can see in this example, there are nine circles. The simulation allows for any number of circles, but I'm trying to make this post as simple as possible for starters. The green dots represent the centers of the circles; the red dots represent the centroids of the three adjacent/connected circles; the black dots represent some intersections (I call these the "outer" intersections) between circles; and the blue lines connect either centroids with other centroids, or centroids to intersections in a particular pattern. In the simulation, the radii of the circles can change and, since I'm applying a distance constraint, the varying sizes of the circles causes the locations (and existence) of the dots and lines to change.
The code that I have at this point is able to identify/calculate the locations of the black dots and the red dots, but I'm having trouble coming up with an algorithm that correctly connects the red and black dots. The diagram I've attached shows the correct connections, but coming up with an algorithm to do this automatically and as the simulation runs has me stumped.
I'll also add that each circle knows which other circles it's in contact with, and what those intersection points are.
Has anyone come across this problem and maybe give me some help?
Thank you and Cheers,
AstroCoder
You do not have the required permissions to view the files attached to this post.
-
bone
- Posts: 231
- Joined: Tue Feb 20, 2007 4:56 pm
Re: Algorithm help / Connecting Centroids
I don't know what information you have available, but it appears that there is a connection between black and red dots any time they share two circles.
-
AstroCoder
- Posts: 3
- Joined: Sat Aug 26, 2017 8:49 pm
Re: Algorithm help / Connecting Centroids
Yes, the black dots are the "outer" intersections between two circles, and the red dots are the centroids of three connected circles.
At each timestep of the simulation, the connections between the centroids and the intersections must be determined. Note that every centroid (red dot) is always connected to three other points which will be either an adjacent centroid or an intersection. Black dots are always only connected to red dots.
I'm sure I have all the info I need, it's just a matter of coming up with the correct algorithm to connect all these points properly.
Cheers,
AstroCoder
At each timestep of the simulation, the connections between the centroids and the intersections must be determined. Note that every centroid (red dot) is always connected to three other points which will be either an adjacent centroid or an intersection. Black dots are always only connected to red dots.
I'm sure I have all the info I need, it's just a matter of coming up with the correct algorithm to connect all these points properly.
Cheers,
AstroCoder
-
bone
- Posts: 231
- Joined: Tue Feb 20, 2007 4:56 pm
Re: Algorithm help / Connecting Centroids
Well, in a simple brute force algorithm form, it's just going to be:
The caveats are:
1) That's inefficient, but that's part of why I mentioned what information you have, because it can be made far more efficient, and
2) You mentioned moving to 3D in your first post, in which case there are more possible cases because the intersections are no longer single points.
Code: Select all
for every red dot
for every black dot
if they share two circles
connect them1) That's inefficient, but that's part of why I mentioned what information you have, because it can be made far more efficient, and
2) You mentioned moving to 3D in your first post, in which case there are more possible cases because the intersections are no longer single points.
-
AstroCoder
- Posts: 3
- Joined: Sat Aug 26, 2017 8:49 pm
Re: Algorithm help / Connecting Centroids
Thank you, bone, for the response. It doesn't look like your suggested algorithm would be able to connect red dots to other red dots.
What other information do you need to improve the efficiency of this algorithm?
Cheers,
AstroCoder
What other information do you need to improve the efficiency of this algorithm?
Cheers,
AstroCoder
-
bone
- Posts: 231
- Joined: Tue Feb 20, 2007 4:56 pm
Re: Algorithm help / Connecting Centroids
Ahh, I misunderstood one sentence in your first post. The previous algorithm could be expanded a bit:
Efficiency could be improved if the circles had a list of the dots that were on them. It might look simple, but the algorithm might end up more complex once you get into the implementation, though. Something like:
Code: Select all
for every red dot
for every red dot
if they share exactly two circles (if they're actually the same red dot, they'll "share" three circles)
connect them
for every black dot
if they share two circles
connect themCode: Select all
for every circle
for every dot on that circle
for every dot on that circle
if they share exactly two circles
connect them-
EtK
- Posts: 7
- Joined: Fri May 31, 2013 10:02 am
Re: Algorithm help / Connecting Centroids
Hello,
I have been on the creative-side of developing this Dynamic Foam project with 'AstroCoder', and here is some extra information for why those centroids need to be connected and form a network.
I. Dynamic Medium
II. Fields and Boids
III. From Boids to a PBD Network
IV. Curling Motion
V. PBD
VI. Conclusion
--
I. Dynamic Medium
The goal of this project is to create a kind on a Zero-player game, a bit like Conway's Game of Life, where cells fluctuate based on surrounding cells, and where the goal to generate Knots within a Dynamic Medium.
To get a sense of such a dynamic network think of a foam with bubbles (volumes) where a micro-fluid runs through the edges (currents). These currents move from high to low pressure, forming circuits. The intensity of the fluid passing the bubbles can make the bubbles shrink or expand. Some currents will be able to line up and form closed circuits.
In 2D these structures are simple loops, in 3D these loops can form strings, and in a next step these strings form again closed-circuits -> knots.

--
II. Fields and Boids
One way to get a model of bubbles and currents going was by using Boid-particles and Fields, which was tried in Processing. Here are short clips to show the interaction:
• http://imgur.com/a/Mp0SG
• https://vimeo.com/user37290268
A. In the first clip the Fields (red circles) keep their size while the small particles flow in between and form a circuit.
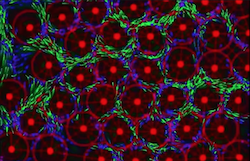
B. In the second version the size of the Fields is influenced by the number of particles within. This gives rise to a dynamic foam with Fields fluctuating. Expand <-> Shrink
--
III. From Boids to a PBD Network
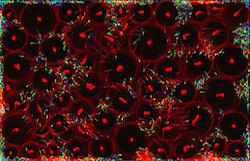
The problem with using Boids is that they have their limitations whereby the quick expansion of Fields causes the particles to be splattered around, interrupting the steady current. (stable flow vs. splashed around)
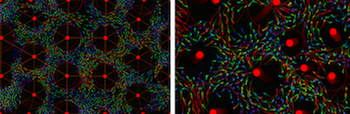
Keeping the Boid-particles flowing is important, because a flow-circuit gives rise to organisational rules such as flows going against each other block each other, others can go along and strengthen each other, similar to an electronic circuit:
So to fix these problems a move to PBD was made and hoping to create a network model (nodes/edges) that replaces the small particles.
The flow replaced by edges:
Fields expanding and shrinking depending on the amount of flow through the edges:
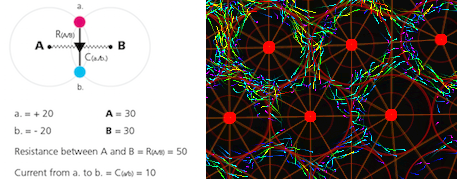
• Having two Fields A.B. and in between from point a. to b. an edge.
• This edges (a.b.) can replace all the boids moving in between (A.B.)
• Edge (a.b.) can represents 1 or 1 million small particles or more, simplification.
• Between Field A. and B. a measurement of tension •-VVVVV-• (A/B)
• The more tension between (A.B.) the less flow there can be in (a.b.)
• Inverse the more flow there is in (a.b.) the less tension between (A.B.)
• The edge (a.b.) runs through the Fields A. and B, cooling or heating up Fields A. and B.
• Through edge (a.b.) runs a current the larger this current the bigger the Fields A. and B. become, expansion vs. shrinking, hot vs. cold, condense vs. vaporise.
The inspiration for the move to 'Position Based Dynamics' came from a talk by Jos Stam where he explained a method explicit on position and using springs:
http://www.birs.ca/events/2014/5-day-wo ... -Stam.html
http://www.birs.ca//workshops//2014/14w ... S-2014.pdf

--
IV. Curling Motion to Strings
At the basis of this Dynamic Foam is the idea to get the bubbles moving through the medium based on self regulated currents between the bubbles:
The mechanics are like a sliding-puzzle where the parts can move to where there is space (created):
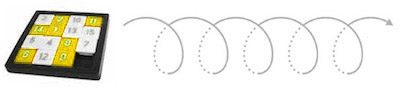
Space can be created by letting the bubbles shrink on one side and expand on the other, so they can move into that created space, and as a result we get fluctuations and a rolling-curling-motion:

Here is a fun animation that is similar to the idea:
https://imgur.com/gallery/xIUGOd9

But for those lemons the input-force is gravity, in my model it are the micro-fluid-currents that effect the size. If the fluid is colder than the bubble than it will condensate and the field will expand; when it is warmer the field will vaporise and shrink. The dynamic curing motion from above, could also turn around and close-loop into knots:
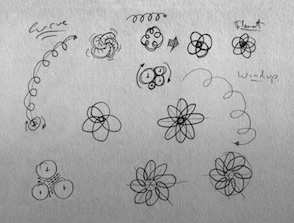
In 3D the wind up curls would be like these folk dansers waving strings:
http://www.youtube.com/watch?v=uvE5yt83WPU (at 1:44)

These strings can turn into knots etc. etc.
--
V. PBD
For a look at the current situation you can check this short clip, where a small network is in place based on centroids, and where the volumes can fluctuate:
http://imgur.com/QSG71hW
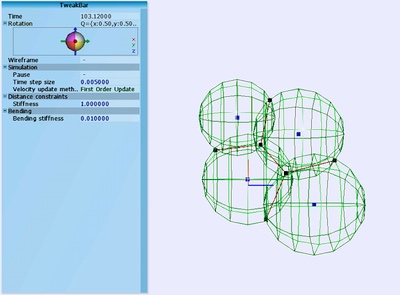
Here is are the project files on GitHub if you would like to have a closer look:
• https://github.com/VirtualOrganics/PBD_ ... Foam_Files
• https://github.com/InteractiveComputerG ... edDynamics (The PDB library that's used)
--
VI. Conclusion
As you have noticed in the OP we are stuck expanding the network and creating the Dynamic Foam. So I'm now looking for a developer who can expand the current program and take it to the next level. It doesn't necessarily need to be in PBD an some Physics Engine might work; where on top of the physics-interactions a network-formula can balance out the weights and regulate the system.
All suggestions and questions are more than welcome!
Best,
m.
I have been on the creative-side of developing this Dynamic Foam project with 'AstroCoder', and here is some extra information for why those centroids need to be connected and form a network.
I. Dynamic Medium
II. Fields and Boids
III. From Boids to a PBD Network
IV. Curling Motion
V. PBD
VI. Conclusion
--
I. Dynamic Medium
The goal of this project is to create a kind on a Zero-player game, a bit like Conway's Game of Life, where cells fluctuate based on surrounding cells, and where the goal to generate Knots within a Dynamic Medium.
To get a sense of such a dynamic network think of a foam with bubbles (volumes) where a micro-fluid runs through the edges (currents). These currents move from high to low pressure, forming circuits. The intensity of the fluid passing the bubbles can make the bubbles shrink or expand. Some currents will be able to line up and form closed circuits.
In 2D these structures are simple loops, in 3D these loops can form strings, and in a next step these strings form again closed-circuits -> knots.

--
II. Fields and Boids
One way to get a model of bubbles and currents going was by using Boid-particles and Fields, which was tried in Processing. Here are short clips to show the interaction:
• http://imgur.com/a/Mp0SG
• https://vimeo.com/user37290268
A. In the first clip the Fields (red circles) keep their size while the small particles flow in between and form a circuit.

B. In the second version the size of the Fields is influenced by the number of particles within. This gives rise to a dynamic foam with Fields fluctuating. Expand <-> Shrink

--
III. From Boids to a PBD Network
The problem with using Boids is that they have their limitations whereby the quick expansion of Fields causes the particles to be splattered around, interrupting the steady current. (stable flow vs. splashed around)

Keeping the Boid-particles flowing is important, because a flow-circuit gives rise to organisational rules such as flows going against each other block each other, others can go along and strengthen each other, similar to an electronic circuit:

So to fix these problems a move to PBD was made and hoping to create a network model (nodes/edges) that replaces the small particles.
The flow replaced by edges:

Fields expanding and shrinking depending on the amount of flow through the edges:

• Having two Fields A.B. and in between from point a. to b. an edge.
• This edges (a.b.) can replace all the boids moving in between (A.B.)
• Edge (a.b.) can represents 1 or 1 million small particles or more, simplification.
• Between Field A. and B. a measurement of tension •-VVVVV-• (A/B)
• The more tension between (A.B.) the less flow there can be in (a.b.)
• Inverse the more flow there is in (a.b.) the less tension between (A.B.)
• The edge (a.b.) runs through the Fields A. and B, cooling or heating up Fields A. and B.
• Through edge (a.b.) runs a current the larger this current the bigger the Fields A. and B. become, expansion vs. shrinking, hot vs. cold, condense vs. vaporise.

The inspiration for the move to 'Position Based Dynamics' came from a talk by Jos Stam where he explained a method explicit on position and using springs:
http://www.birs.ca/events/2014/5-day-wo ... -Stam.html
http://www.birs.ca//workshops//2014/14w ... S-2014.pdf

--
IV. Curling Motion to Strings
At the basis of this Dynamic Foam is the idea to get the bubbles moving through the medium based on self regulated currents between the bubbles:

The mechanics are like a sliding-puzzle where the parts can move to where there is space (created):

Space can be created by letting the bubbles shrink on one side and expand on the other, so they can move into that created space, and as a result we get fluctuations and a rolling-curling-motion:

Here is a fun animation that is similar to the idea:
https://imgur.com/gallery/xIUGOd9

But for those lemons the input-force is gravity, in my model it are the micro-fluid-currents that effect the size. If the fluid is colder than the bubble than it will condensate and the field will expand; when it is warmer the field will vaporise and shrink. The dynamic curing motion from above, could also turn around and close-loop into knots:

In 3D the wind up curls would be like these folk dansers waving strings:
http://www.youtube.com/watch?v=uvE5yt83WPU (at 1:44)

These strings can turn into knots etc. etc.
--
V. PBD
For a look at the current situation you can check this short clip, where a small network is in place based on centroids, and where the volumes can fluctuate:
http://imgur.com/QSG71hW

Here is are the project files on GitHub if you would like to have a closer look:
• https://github.com/VirtualOrganics/PBD_ ... Foam_Files
• https://github.com/InteractiveComputerG ... edDynamics (The PDB library that's used)
--
VI. Conclusion
As you have noticed in the OP we are stuck expanding the network and creating the Dynamic Foam. So I'm now looking for a developer who can expand the current program and take it to the next level. It doesn't necessarily need to be in PBD an some Physics Engine might work; where on top of the physics-interactions a network-formula can balance out the weights and regulate the system.
All suggestions and questions are more than welcome!
Best,
m.
-
bone
- Posts: 231
- Joined: Tue Feb 20, 2007 4:56 pm
Re: Algorithm help / Connecting Centroids
Looks like a fascinating project!
We brushed on this earlier, but how does the transition from 2-D to 3-D affect those intersections (the red and black dots from the original post)? I can't immediately picture if there would still be only two classifications of intersections.
Anyway, wish I could help more but I'm solidly committed to other projects.
We brushed on this earlier, but how does the transition from 2-D to 3-D affect those intersections (the red and black dots from the original post)? I can't immediately picture if there would still be only two classifications of intersections.
Anyway, wish I could help more but I'm solidly committed to other projects.
-
EtK
- Posts: 7
- Joined: Fri May 31, 2013 10:02 am
Re: Algorithm help / Connecting Centroids
Thanks!bone wrote:Looks like a fascinating project!
Indeed when you go into 3D and you look at a foam, then the edges (ribs) can be between 3 or 4 spheres and so the centroids also depend on more 'dots', it becomes more complicated but the concept stays the same. But for now 2D is good enough to experiment.We brushed on this earlier, but how does the transition from 2-D to 3-D affect those intersections (the red and black dots from the original post)? I can't immediately picture if there would still be only two classifications of intersections.
Drop your other projects, this is a once in a lifetime opportunity!Anyway, wish I could help more but I'm solidly committed to other projects.
-
RandyGaul
- Posts: 43
- Joined: Mon May 20, 2013 8:01 am
- Location: Redmond, WA
Re: Algorithm help / Connecting Centroids
I would point out the interior of the bubbles form a 3D Voronoi diagram.
-
EtK
- Posts: 7
- Joined: Fri May 31, 2013 10:02 am
Re: Algorithm help / Connecting Centroids
Yes, that's it.RandyGaul wrote:I would point out the interior of the bubbles form a 3D Voronoi diagram.
I already knew, but thanks for bringing it up, it is a interesting reference.
It has lead me to check the Voronoi diagram algorithm. The method most used is 'Edge Flip Algorithm for Delaunay Triangulation', and for DL I found this lecture:
http://www.cs.uu.nl/docs/vakken/ga/slides9alt.pdf (1.2 Mb)

An other cool reference is this paper on 'Quasi-static Simulation of Foam in the Vertex Model' that uses a dual mesh based on centroids:
https://youtu.be/DN23diqRAGY (clip)
http://image.diku.dk/kenny/download/vedel_larsen.10.pdf (7.2 Mb)


--
Anyway, this is far above my head, if a mathematician among you can think of how to connect the dots, and come up with a (partial) solution for the network, than don't hesitate to contact me.
-
RandyGaul
- Posts: 43
- Joined: Mon May 20, 2013 8:01 am
- Location: Redmond, WA
Re: Algorithm help / Connecting Centroids
You can find your planes by performing plane slicing. Start with a simple convex shape, like an AABB, and slice it with many planes. Something like this:
The Slice function can be tricky to write, but with some hard work you can implement it yourself. The trick is to store indices of points along with each slice, so the final hull can store all bounding planes and the indices of each point involved.
Once all hulls are gathered up they are already connected in a graph data structure. Each hull contains a list of planes. Each plane contains two indices to another hull. Hulls are identified by the index of the associated point (index i in the above code). The graph can be traversed from hull, to plane, to adjacent hull.
This algorithm should be able to construct the Voronoi diagram.
Note: I've never implemented the Voronoi diagram function itself, but have implemented plane slicing like I described here, so it should all work.
Of course, this algorithm does not find the radius of a given point. For example, the exterior sites in your diagrams are surrounded by a spherical surface; you would need another algorithm to find these surfaces somehow. You would also need to prune leftover planes from the initial AABB (which can be represented in the final hull with -1 indices in the above algorithm), and replace them with the spherical surface somehow.
This is an O(N*N) algorithm.
Edit:
You could also try using a library to find the Voronoi Diagram. For example qhull library can be used to achieve this in O(N*log(N)) time.
Code: Select all
AABB bounds = WrapAllPoints(points, extra_radius);
std::vector<ConvexHull> hulls;
for (int i = 0; i < points.size(); ++i)
{
Point a = points[i];
ConvexHull hull;
hull.Init(bounds);
for (int j = 0; j < points.size(); ++j)
{
Point b = points[j];
Plane p;
p.normal = Normalize(b - a);
p.distance = Dot(p.normal, a);
Slice(hull, p, i, j);
}
hulls.push_back(hull);
}
Once all hulls are gathered up they are already connected in a graph data structure. Each hull contains a list of planes. Each plane contains two indices to another hull. Hulls are identified by the index of the associated point (index i in the above code). The graph can be traversed from hull, to plane, to adjacent hull.
This algorithm should be able to construct the Voronoi diagram.
Note: I've never implemented the Voronoi diagram function itself, but have implemented plane slicing like I described here, so it should all work.
Of course, this algorithm does not find the radius of a given point. For example, the exterior sites in your diagrams are surrounded by a spherical surface; you would need another algorithm to find these surfaces somehow. You would also need to prune leftover planes from the initial AABB (which can be represented in the final hull with -1 indices in the above algorithm), and replace them with the spherical surface somehow.
This is an O(N*N) algorithm.
Edit:
You could also try using a library to find the Voronoi Diagram. For example qhull library can be used to achieve this in O(N*log(N)) time.